|
|
|
1.
Aufgabe:
a)
(1) 137 + 124 + 123 + 136
= (137 + 123) + (124 + 136)
= 260 + 260 = 520
(2) [127 + (285 + 123)] + 147
= [(127 + 123) + 285] + 147
= (250 + 285) + 147
= 535 + 147 = 682
b)
74183
– 6384
– 8553
– 8076
-----------
= 51170
2.
Aufgabe:
a)
(1) (150 + 75) + (150 - 75)
= 225 + 75 = 300
(2) (283 - 156) - (37 + 78)
= 127 - 115 = 12
b)
(99 + 15) - (33 - 19) = 114 - 14 = 100
Aufgabe in Wortform:
Subtrahiere von der Summe aus 99 und 15 die Differenz der Zahlen
33 und 19!
3.
Aufgabe:
a) 88
+ 87 + 86 = 261
b)
Der Wert der Summe ändert sich nicht!
c)
Der Wert der Differenz ändert sich nicht!
4. Aufgabe:
|
a)
(1) 18 + X = 32
X = 32 - 18 = 14
(2) X - 35 = 25
X = 35 + 25 = 60
(3) 38 - X = 17
X = 38 - 17 = 21
|
b) Man
muss 133 zu "0" addieren,
um 133 zu erhalten:
0 + 133 = 133
c)
Rechnung:
35.550
- 2.130
- 630
- 7.200
- 510
- 412
1 2 1 1
-----------
24.668
Antwort:
Es sind noch 24.668 Flaschen im Lager.
|
|
Zurück zur Klassenarbeit

|
Mathematik
Klasse 5 |
|
Ganze Zahlen
-
Grundwissen |
Dies ist ein
Ausschnitt aus dem Artikel "Ganze Zahlen" aus unserem Projekt
lernstunde.de, dort findet ihr Zusammenfassungen von Unterrichtseinheiten.
Ganze Zahlen Definitionen Die Menge 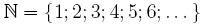 heißt Menge der natürlichen Zahlen. heißt Menge der natürlichen Zahlen. Die Menge 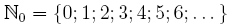 heißt Menge der natürlichen Zahlen einschließlich der Null. heißt Menge der natürlichen Zahlen einschließlich der Null. Die Menge 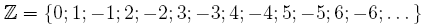
heißt Menge der ganzen Zahlen. Die Begriffe negativ und positiv: 
Von zwei ganzen Zahlen a,b heißt -
a kleiner als b, geschrieben a < b, wenn a auf der Zahlengeraden links von b liegt. Beispiele: – 6 < –5 oder –5 < 4 oder 8 < 9 -
a größer als b, geschrieben a > b, wenn a auf der Zahlengeraden rechts von b liegt. Beispiele: 5 > 4 oder 2 > –3 oder –1 > –2 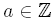 heißt positiv, wenn a > 0 gilt und negativ, wenn a < 0 gilt. heißt positiv, wenn a > 0 gilt und negativ, wenn a < 0 gilt.
Auf der Zahlengeraden liegen die positiven Zahlen rechts von der Null und die negativen links von der Null. |  Merke Merke
Für alle 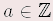 gilt: gilt: | 0 – a | = | – a | | –(–a) | = | a | | (– 1) · a | = | – a | Insbesondere: – 0 = + 0 = 0 und –(–1) = 1 und (–1) · (–1) = 1. | Beispiele | a) | 0 – 2 | = | –2 | b) | 0 – (–2) | = | 2 | | c) | –(–2) | = | 2 | d) | –(+2) | = | – 2 | | e) | (– 1) · 2 | = | – 2 | f) | (–1) · (–2) | = | 2 | |  Merke Merke
Für alle 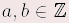 gilt: gilt: | a + (– b) | = | a – b | | a – (+b) | = | a – b | | a – (–b) | = | a + b | | Beispiele
... der Original-Artikel ist etwa 3 Mal länger und natürlich auch kostenlos verfügbar!
Hier geht's zum kompletten
Artikel zur Unterrichtseinheit Ganze Zahlen...
|
|
|