|
Zusammenfassung
Integralrechnung
Die Integralrechnung ist eine
Art Flächenberechnung. Dabei handelt es sich um den Flächeninhalt unter
krummlinigen Kurven von Funktionen. Solche Flächen können nicht einfach mit
Länge mal Breite berechnet werden.
Das Problem solcher Flächenberechnung ist schon sehr alt und wurde bereits
von ARCHIMEDES (287 - 212 vor unserer Zeit) untersucht. ARCHIMEDES
hat z.B. berechnet, wie groß der Flächeninhalt unter einer Parabel ist. Das
ist umso erstaunlicher, als es zu seiner Zeit überhaupt keine praktische
Verwendung für diese Rechnungen gab.
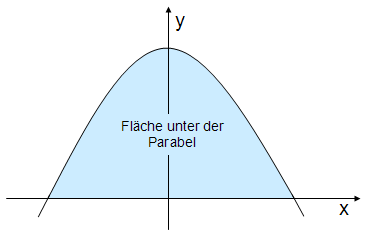
Eine grundlegende Idee für diese
Flächenberechnung ist folgende: Man versucht, eine "Kurvenfläche" mit
solchen Flächen auszufüllen, die man leicht berechnen kann. Das sind vor
allem Rechteck- und Dreieickflächen. Dann summiert man diese Teilflächen und
erhält die Gesamtfläche.
ARCHIMEDES hat die Parabelfläche
ausgefüllt mit gleichschenkligen Dreiecken. Die noch frei gebliebene Fläche
wird immer kleiner und wird mit einem immer kleineren Dreieck ausgefüllt.
Theoretisch kann man mit
allerkleinsten Dreiecken die Parabelfläche ganz ausfüllen. Allerdings nur,
wenn man das unendlich fortsetzt, denn es zeigt sich, dass immer noch Platz
frei bleibt, so klein das Dreieck auch wird. Man bekommt mit dieser Methode
doch schon recht genaue Ergebnisse.
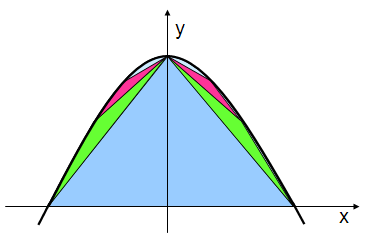
Weil die Fläche sozusagen
ausgeschöpft wird, nennt man diese Methode auch "Ausschöpfungs-Methode" (mit
Fremdwort: Exhaustions-Methode).
Man sieht, dass statt der Dreiecke auch Rechtecke oder Trapeze oder
Kombinationen solcher Figuren genommen werden können. Die Flächen lassen
sich leicht berechnen und müssen nur summiert werden. Das Ergebnis ist aber
immer nur hinreichend genau.
Die Ausschöpfungs-Methode ist keine eigentliche Integralrechnung, denn die
Integralrechnung beruht auf einer völlig anderen Methode.
Heute wird die Integralrechnung im wesentlichen so benutzt, wie sie von
G.W.LEIBNIZ (1646 - 1716) und I.NEWTON (1643 - 1727) entwickelt
wurde.
Man kann feststellen, dass die Integralrechnung rein rechnerisch die
Umkehr-Rechnung der Differentialrechnung ist, weshalb beide auch zur
Infinitesimal-Rechnung zusammengefasst werden.
Während bei der Differenzierung einer Funktion die 1.Ableitung ermittelt
wird, kann man sich die Integration so vorstellen:
Eine Funktion zu integrieren (d.h. die Fläche unter der Funktionskurve zu
berechnen) heißt, sich diese Funktion als 1.Ableitung zu denken. Nun sucht
man eine dazu gehörige Funktion, die - wenn man sie ableitet - ebenjene
1.Ableitung (also die Ausgangsfunktion) ergeben würde. Diese andere Funktion
heißt Stammfunktion.
Beispiel:
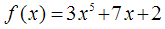
Die Stammfunktion lautet:
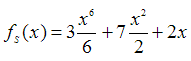
Würde man davon die 1.Ableitung
bilden, dann erhält man genau die erste Funktion.
Das ist das Prinzip der Integration von Funktionen.
Diese Methode ist im Unterschied zur Ausschöpfungs-Methode in ihrem Vorgehen
algebraisch und nicht geometrisch. Während die Ausschöpfung mit
geometrischen Figuren arbeitet, verwendet die Integralrechnung algebraische
Ausdrücke, also letztendlich Gleichungen.
Für die Integration gibt es eine
spezielle Schreibweise:
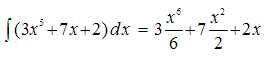
Allgemein:
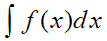
bedeutet:
Integral der Funktion f(x), also geometrisch die Fläche unter dieser
Funktionskurve. Viele Stammfunktionen lassen sich leicht finden, aber noch
mehr lassen sich nur schwer und manche gar nicht finden. So ist z.B.
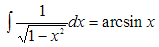
Zudem gibt es keinen
eigentlichen Rechenweg (Algorithmus), um zur Stammfunktion zu kommen,
sondern nur Regeln. Deshalb sind in Tabellen häufige und bekannte
Stammfunktionen oder Grundintegrale aufgeführt. Außerdem gibt es im Internet
Integral-Online Rechner.
Nun folgen einige Beispiele von Flächen unter Funktionskurven zu sehen,
deren Flächeninhalt berechnet werden könnte. Diese Aufgabenstellungen werden
dir in der Integralrechnung also begegnen:
1. Der Flächeninhalt wird vom
Graph der quadratischen Funktion und der x-Achse eingeschlossen:
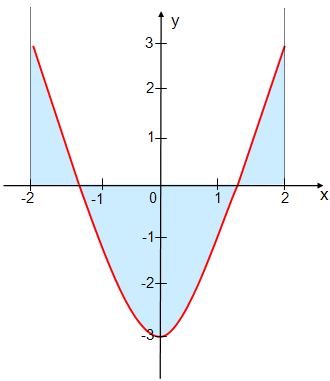
2. Der Flächeninhalt wird vom
Graph der kubischen Funktion und der x-Achse eingeschlossen:
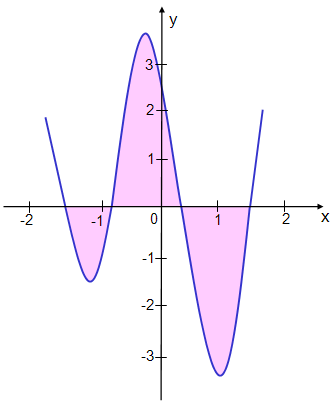
3. Der Flächeninhalt wird von
den Graphen zweier quadratischer Funktionen eingeschlossen:
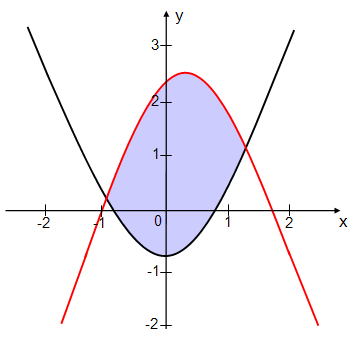
4. Flächeninhalt zwischen den
Graphen zweier quadratischer Funktionen und über deren Schnittpunkte hinaus:
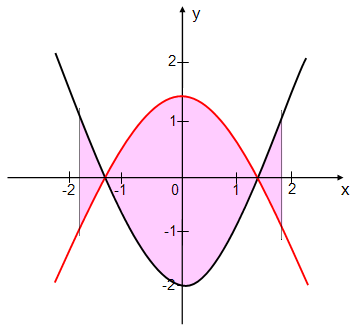
5. Der Flächeninhalt wird
zwischen dem Graphen einer Funktion und einer Geraden eingeschlossen:
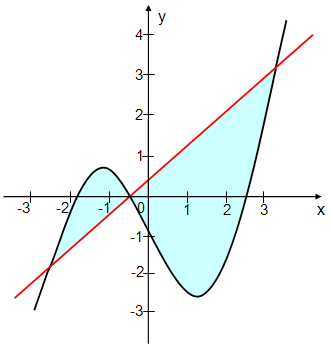
6. Der Flächeninhalt liegt
zwischen den Graphen zweier Funktionen, die sich nicht schneiden:
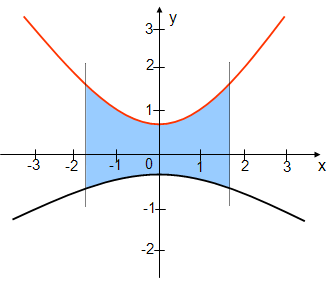
Das bestimmte Integral
Der Flächeninhalt wird innerhalb eines Intervalls bestimmt. Dieses
Intervall hat immer eine untere und eine obere Grenze. Die Grenzen
entsprechen bestimmten x-Werten, also Stellen auf der x-Achse.
Innerhalb dieser Intervallgrenzen verläuft die Funktionskurve und damit die
Fläche. Weil die Grenzen genau bestimmt sind, spricht man auch von einem
bestimmten Integral.
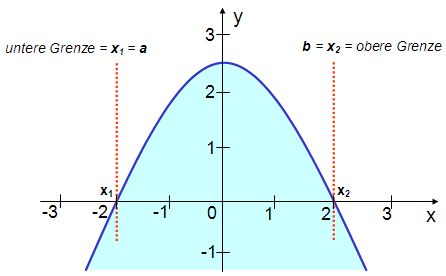
Die Intervallgrenzen eines
bestimmten Integrals werden in der Schreibweise verdeutlicht:
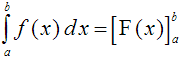
Unter dem Integralzeichen steht
immer die untere Grenze, darüber die obere Grenze. Die eckigen Klammern
bedeuten: Intervall in den Grenzen von a bis b. Das große F
bedeutet: Stammfunktion von f(x).
Das Berechnen des Flächeninhalts
ist nicht schwer, wenn man die Stammfunktion hat.
Man setzt in die Stammfunktion die Intervallgrenzen als x-Werte ein.
Weil stets zwei solche x-Werte gegeben sind, erhält man zweimal die
Stammfunktion jeweils mit der unteren und mit der oberen Intervallgrenze.
Nun subtrahiert man die Stammfunktion mit der unteren Grenze von der mit der
oberen Grenze und erhält eine Zahl, die dem Flächeninhalt entspricht.
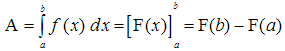
Man nennt diese Flächeninhalt-Zahl auch Maßzahl.
Sie hat keine Einheit, weil auch die Begrenzungslinien der Fläche keine
Einheiten haben.
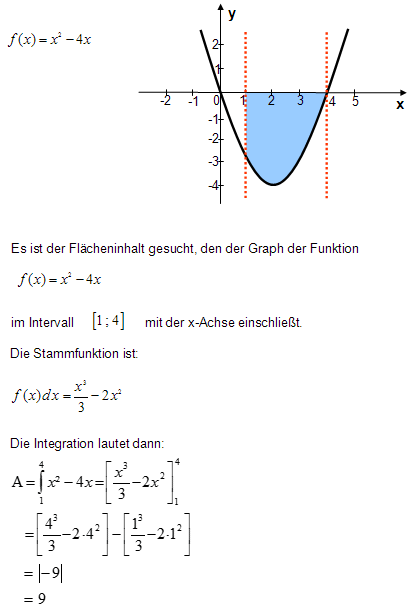
Beispiel für eine Aufgabe mit
bestimmtem Integral:
Eine Funktion kann mehrere
Nullstellen haben und die eingeschlossene Fläche
kann über oder unter
der x-Achse liegen.
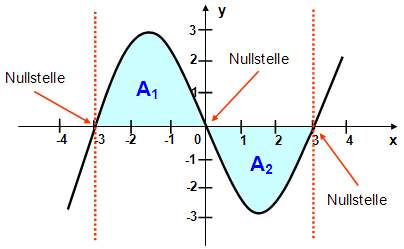
Bei der Integralrechnung gibt es
keine "negativen" Flächen, es wird immer der absolute Betrag des Ergebnisses
genommen.
Es kann nicht über Nullstellen hinweg integriert werden. Wenn die Funktion
Nullstellen hat, werden die einzelnen Teilflächen jede für sich integriert.
Die Teilflächen werden zur Gesamt-Integral-Fläche summiert.
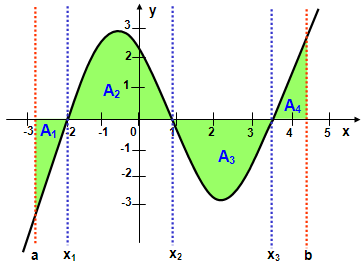
Innerhalb des Intervalls werden
die Teilflächen integriert und zur Gesamtfläche summiert.
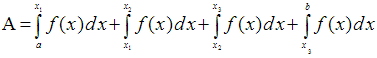
Ähnlich wie bei Nullstellen,
muss man auch die Fläche integrieren,
die von zwei Graphen
eingeschlossen wird, die sich schneiden.
Auch hier darf nicht über die Schnittpunkte hinweg integriert werden.
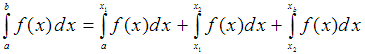
Bei Funktionen,
deren Graphen sich nicht
schneiden, wird die
Fläche zwischen den Graphen so berechnet:
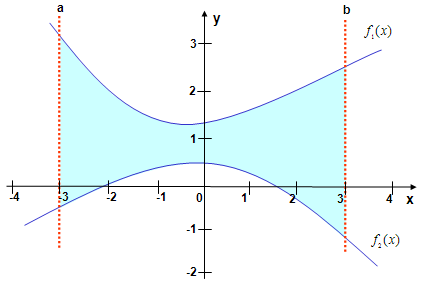
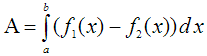
Vor dem Integrieren wird die
"untere" Funktion von der "oberen" Funktion subtrahiert.
Das Ergebnis (Differenz) wird als eine Funktion innerhalb des
Intervalls integriert.
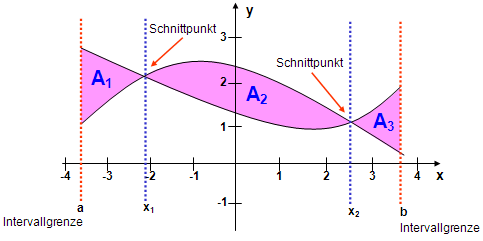
Bei Funktionen,
deren Graphen sich schneiden,
wird die Fläche zwischen den Graphen so berechnet:
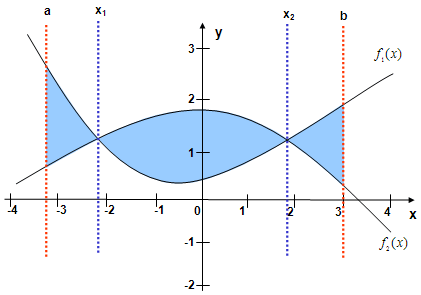
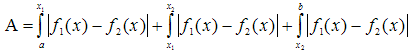
Für jede Teilfläche wird die
"untere" von der "oberen" Funktion subtrahiert und die Differenz-Funktion
integriert. Alle Teil-Integrale werden summiert. Alle Flächen haben absolute
Beträge als Maßzahlen. Es darf nicht über die Schnittpunkte hinweg
integriert werden.
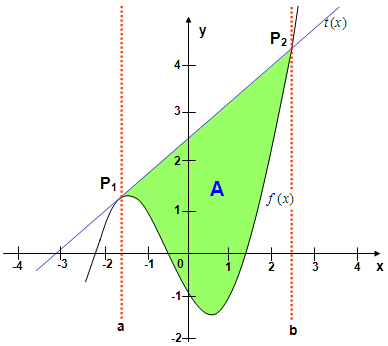

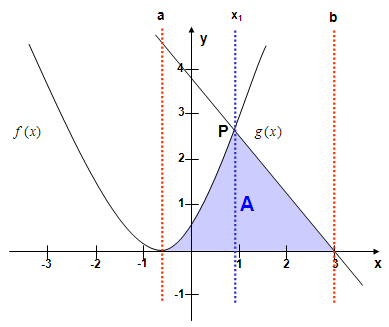
Der Graph der Funktion und eine
Gerade schneiden sich in einem Punkt und schließen mit der x-Achse eine
Fläche ein. Es müssen die Nullstellen beider Funktionen und ihr Schnittpunkt
ermittelt werden. Das Gesamtintervall besteht aus zwei Teilintervallen, die
sich im Schnittpunkt "berühren"
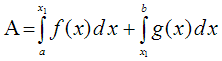 |