Funktionsuntersuchung

Erfahre mehr über Funktionsscharen, newtonsches Näherungsverfahren und Rotationsvolumen

Funktionsscharen

Funktionsscharen sind eine Gruppe von Funktionen, die eine gemeinsame Eigenschaft oder einen gemeinsamen "Bauplan" teilen, aber durch einen oder mehrere Parameter voneinander unterschieden werden. Diese Parameter können in der Funktion wie eine Art "Schlüssel" wirken, der die Funktion in verschiedenen Situationen anpasst.
Ein einfaches Beispiel für eine Funktionsschar ist die Familie der linearen Funktionen:
f(x) = m * x + b
Hier sind "m" und "b" die Parameter, die die Funktionsschar definieren. Die verschiedenen Funktionen in dieser Schar haben unterschiedliche Steigungen (m) und y-Achsenabschnitte (b), aber alle folgen der gleichen grundlegenden Formel.
Ein weiteres Beispiel ist die Familie der quadratischen Funktionen:
g(x) = a * x^2 + b * x + c
In diesem Fall sind "a", "b" und "c" die Parameter, die die Funktionsschar definieren. Die verschiedenen Funktionen in dieser Schar haben unterschiedliche Koeffizienten für die x^2-, x- und konstanten Terme, aber alle folgen der gleichen grundlegenden Formel.

Eine Funktionsschar beschreibt mehrere miteinander verwandte Funktionen. Sie entstehen wenn du für einen Parameter in der Funktion verschiedene Werte einsetzten kannst.

Newtonsches Näherungsverfahren

Das Newtonsche Näherungsverfahren ist eine hilfreiche Technik, um Näherungslösungen für Gleichungen zu finden, bei denen eine exakte Lösung schwierig oder unmöglich zu berechnen ist. Dieses Verfahren eignet sich besonders für Gleichungen höheren Grades oder solche, die Transzendental- oder Logarithmusfunktionen enthalten. Die grundlegende Idee besteht darin, eine Annäherung an die Lösung der Gleichung zu finden und diese schrittweise zu verbessern, bis eine ausreichend genaue Lösung erreicht ist. Zunächst wählt man einen Startwert (x0) als ungefähre Lösung der Gleichung. Anschließend berechnet man die Steigung der Funktion f(x) an der Stelle x0, indem man die Ableitung der Funktion (f'(x)) an dieser Stelle auswertet. Nach der Berechnung der Steigung findet man die Tangente an der Stelle x0 und folgt dieser Tangente, bis sie die x-Achse schneidet. Der Schnittpunkt mit der x-Achse gibt einen neuen Näherungswert (x1) für die Lösung der Gleichung. Diesen Prozess wiederholt man mit dem neuen Näherungswert (x1), um einen noch besseren Näherungswert (x2) zu erhalten. Man wiederholt diesen Vorgang, bis die Lösung genau genug ist oder die Differenz zwischen zwei aufeinanderfolgenden Näherungswerten sehr klein wird.

Durch das Newtonsche Näherungsverfahren kann man Lösungen für komplizierte Gleichungen finden, indem man verbesserte Näherungswerte berechnet.

Rotationsvolumen

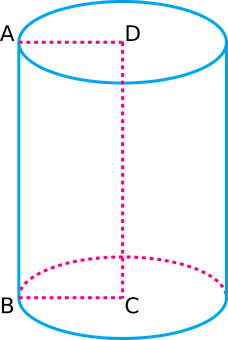
Ein Rotationsvolumen ist ein dreidimensionales Objekt, das entsteht, wenn man eine zweidimensionale Fläche um eine gerade Achse dreht. Man kann sich das als das Volumen vorstellen, das entsteht, wenn man eine Figur wie eine Papierform oder einen Zeichnung auf einer Ebene nimmt und sie dann um eine Linie herum dreht. Diese Linie wird als Rotationsachse bezeichnet. Ein einfaches Beispiel ist das Volumen einer Zylinderform. Um dies zu visualisieren, können wir eine rechteckige Fläche nehmen, bei der eine Seite die Höhe des Zylinders darstellt und die andere Seite den Radius des Zylinders (siehe Abbildung). Wenn wir diese Fläche um die Achse entlang der Höhe des Zylinders drehen, erhalten wir das Rotationsvolumen.
Um das Volumen eines Rotationskörpers zu berechnen, gibt es verschiedene Methoden, wie die Scheibenmethode, die Schalenmethode oder die Integration. Eine der gebräuchlichsten Methoden ist die Verwendung von Integralen.

Wenn eine Fläche um eine Achse rotiert entsteht ein Rotationskörper.