Für die Bestimmung der Nullstellen einer ganzrationalen Funktion f ist
es günstig, wenn der Funktionsterm in faktorisierter Form vorliegt.
Diese erhalten wir durch Ausklammern.
Ein Beispiel:
Faktorisieren Sie den Term x4 +x3
– 2x2 + 4x – 24. Klammern Sie dazu in
einem ersten Schritt den Faktor
(x – 2) und in einem zweiten den Faktor
(x + 3) aus.
Wir formen den Term so um, dass wir den gewünschten Faktor ausklammern
können.
Dazu ergänzen wir jeweils geschickt so, dass zwei aufeinander folgende
Summanden den Faktor enthalten:
x4 + x3
– 2x2 + 4x – 24 =
x4 – 2x3
+ 3x3 – 6x2
+ 4x2 – 8x
+ 12x – 24 =
= x3·(x – 2) +3x2·(x
– 2)+ 4x·(x – 2) + 12·(x – 2) = (x – 2)·(x3
+ 3x2 + 4x + 12)
(x – 2)·(x3 + 3x2
+ 4x + 12) = (x – 2)[x2·(x + 3) + 4·(x
+ 3)] = (x – 2)·(x + 3)·(x2 + 4)
Dem faktorisierten Term können wir jetzt z. B. leicht die Nullstellen
entnehmen.
Beim Ausklammern können wir nach dem folgenden Schema vorgehen:
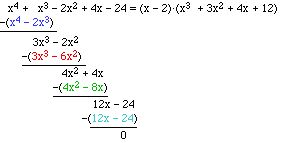
Dabei erhalten wir die oben erzeugten Summanden praktisch durch
„Zurückmultiplizieren“ mit den ausgeklammerten Faktoren.
Wegen der starken Ähnlichkeit zum schriftlichen Divisionsverfahren
spricht man hier von Polynomdivision.
Bleibt noch ein Problem zu klären: woher wissen wir, welcher Faktor sich
ausklammern lässt?
Wie schon bekannt ist, lässt sich das Polynom f(x) zerlegen in (x – x0)·q(x)
, wenn x0 eine Nullstelle der
zugehörigen Funktion f ist.
Hier hilft nur gezieltes Probieren weiter, das uns durch den
folgenden Satz erleichtert wird:
Ist f(x) ein Polynom mit nur ganzzahligen Koeffizienten und den
absoluten Summanden a0, dann ist jede
ganzzahlige Nullstelle der zugehörigen ganzrationalen Funktion f ein
Teiler von a0.
Wir können uns beim Probieren also auf die Teiler des absoluten Summaden
beschränken, wenn wir durch geschicktes Multiplizieren oder Ausklammern
der erreicht haben, dass nur noch ganzzahlige Exponenten auftreten.
Beispiel:
Faktorisieren Sie x5 + 3x4
+
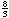 x3
– x –
 .
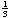Wir klammern zunächst den Faktor
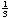aus und erhalten
x5 + 3x4
+
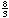 x3
– x –
=
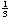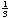 ·(3x5
+ 9x4 + 8x3
– 3x – 1)
Das Polynom 3x5 + 9x4
+ 8x3 – 3x – 1 enthält nur noch
ganzzahlige Koeffizienten, also können wir den Satz anwenden und sehen,
dass die einzigen möglichen ganzzahligen Nullstellen bei +1 oder bei –1
liegen können.
Achtung: Der Satz sagt nicht aus, dass es überhaupt ganzzahlige
Nullstellen geben muss, er sagt nur: wenn es eine ganzzahlige
Nullstelle gibt, dann ist sie unter den Teilern des absoluten
Summanden zu finden.
Im Beispiel gibt es also nur die beiden Kandidaten +1 und –1.
3(+1)5 + 9(+1)4
+ 8(+1)3 – 3(+1) – 1 = 3 + 9 + 8 – 3 –
1 = 16 ‚ 0
3(–1)5 + 9(–1)4
+ 8(–1)3 – 3(–1) – 1 = –3 + 9 – 8 + 3 –
1 = 0
Der Faktor (x – (–1)) = (x + 1) lässt sich also Ausklammern.
Führen Sie die Rechnung durch.
Beachten Sie dabei:
Aus Gründen der Übersichtlichkeit empfiehlt es sich, jedes Polynom so
zu schreiben, dass keine x-Potenz zwischen dem Grad und der 0
ausgelassen wird.
Das Polynom 3x5 + 9x4
+ 8x3 – 3x – 1 sollte also so
geschrieben werden:
3x5 + 9x4
+ 8x3 + 0·x2
– 3x – 1
bevor die Division ausgeführt wird.
Endergebnis:
x5 + 3x4
+
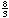 x3
– x –
=
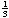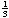 ·(3x2
– 1)·(x + 1)3
Aufgaben zur Bestimmung von
Nullstellen ganzrationaler Funktionen
Bestimmen Sie jeweils alle Nullstellen der folgenden ganzrationalen
Funktionen:
a) f: x
 x3
+ x2 – 9x – 9 |
b) f: x
 x4
– 2,5x3 + 0,5x2
+ x |
c) f: x
 0,5x4
+ 0,5x3 + x2
+ 2x – 4 |
d) f: x
 (x3
– 1)·(x3 + 1,7x2
+ 0,1x – 0,6) |
e) f: x
 x4
+ x3 – x2
+ x – 2 |
f) f: x
 x4
– 2x3 + 2x – 1
|
g) f: x
 3x3
+ 6x2 – 3x – 6 |
h) f: x
 x4
+ 10,25x2 + 24,5
|
i) f: x
 x3
+ x2 – 17x + 15 |
j) f: x
 2x4
– 6x3 + 6x2
– 2x |
Die Lösungen:
| a) x1= –3, x2
= –1 ; x3 = 3 |
b) x1
= –0,5 ; x2 = 0 ; x3
= 1 ; x4 = 2 |
| c) x1 = –2 ; x2
= 1 |
d) x1
= –1,2 ; x2 = –1 ; x3
= 0,5 ; x4 = 1 |
| e) x1 = –2 ; x2
= 1 |
f) x1
= –1 ; x2 = 1 (dreifache
Nullstelle) |
| g) x1 = –2 ; x2
= –1 ; x3 = 1 |
h) keine Nullstellen |
| i) x1 = –5 ; x2
= 1 ; x3 = 3 |
j) x1
= 0 ; x2 = 1 (dreifache
Nullstelle) |
|
