Funktionen
Grundwissen Klasse 11 bis Abitur
Tatsache 1
Punkt auf Graph f - Koordinaten erfüllen
Funktionsgleichung
Wenn ein Punkt auf einem Graphen liegt, so müssen
seine Koordinaten die Funktionsgleichung erfüllen.
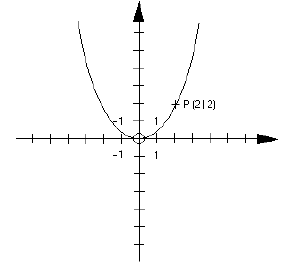
Beispiel:
f(x) = 0,5 x²
P (2/2)
→ x = 2
f(x) = 0,5 *
4 = 2 → y = 2
Tatsache 2
Geraden stehen senkrecht aufeinander: m1
* m2 = -1
Wenn zwei Geraden senkrecht aufeinander stehen, so
ergibt das Produkt ihrer Steigungen immer -1.

Beispiel:
f(x)
= -2x
g(x) = 0,5 x
-2 * 0,5 = -1
Tatsache 3
Umkehrfunktionen:
3.1
Definitions- und Wertebereich
3.2 Wann gibt es eine Umkehrfunktion?
3.1 Definitions- und Wertebereich
Da bei der Bildung der Umkehrfunktion einer Funktion,
durch die Spiegelung der Graphen an der Winkelhalbierenden des 1. und 3.
Quadranten, die x- und y- Werte vertauscht werden, werden auch der
Definitions- und Wertebereich vertauscht.
Folglich gilt:
ID (Definitionsmenge) der Funktion f =
IW (Wertemenge) der Umkehrfunktion f -1
IW (Wertemenge) der Funktion f
= ID (Definitionsmenge) der Umkehrfunktion f -1
3.2 Umkehrbarkeit einer Funktion
Eine Funktion ist dann umkehrbar, wenn sie in ihrem gesamten
Definitionsbereich streng monoton steigend ist (analog wenn f im gesamten ID
streng monoton fallend ist)
Die Umkehrung dieses Satzes gilt
allerdings nicht!!
So muss eine Funktion, die umkehrbar ist, noch lange nicht monoton sein.
Beispiel:
Die Funktion f (x) =
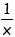 ist zwar umkehrbar (f
-1 = ist zwar umkehrbar (f
-1 = 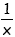 ) aber
nicht streng monoton abnehmend ) aber
nicht streng monoton abnehmend
in IR \ {0} (Vgl. Tatsache 5)
Tatsache 4
Überblick über Graphen von Polynomfunktionen:
4.1
Parabeln
4.2 Funktionen dritten Grades
4.3 Funktionen vierten Grades
4.1 Parabeln f(x) = ax² +
bx + c
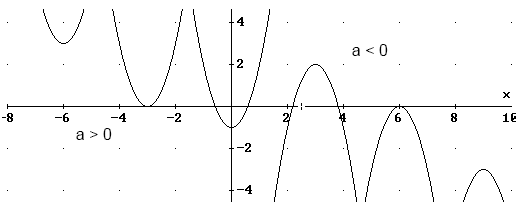
Durch Änderung von a wird die Parabel enger (IaI > 1)
oder weiter (IaI <1)
das Vorzeichen bestimmt, ob die Parabel nach oben (a > 0) oder nach
unten (a < O) geöffnet ist.
4.2 Funktionen dritten Grades f(x)= ax³
+ bx² +cx + d
Verhalten im Unendlichen:
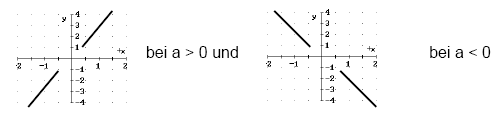
Unterschiede in Art und Anzahl der Nullstellen:
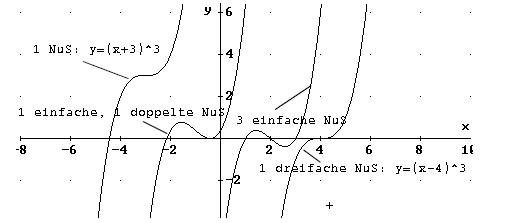
Graphen dritten Grades haben mindestens 1 und höchstens drei Nullstellen.
4.3 Funktionen vierten Grades f(x) = ax4
+bx³ + cx² +dx + e
Verhalten im Unendlichen:
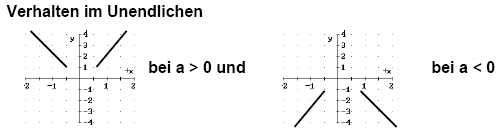
Unterschiede in Anzahl und Art der Nullstellen:
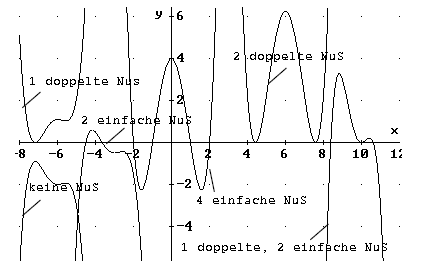
Das sind natürlich noch lange nicht alle
Möglichkeiten.
Tipp: Experiment mit Derive
Graphen nach rechts/ links verschieben, indem man x
durch (x + a) substituiert, nach oben/ unten indem man zum Funktionsterm a
addiert.
Will man doppelte Nullstellen, so bestimmt man Maxima oder Minima und
addiert, bzw. subtrahiert sie vom Funktionsterm.
Beispiel:
Diese Funktion hat genau 2 einfache Nullstellen:
f(x) = x4 - x = x *
(x³ - 1)
Die erste Nullstelle ist x= 0.
Durch Ausprobieren finden wir als 2. Nullstelle x = 1.
Tatsache 5
Die Funktion f(x) =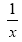 fällt (negative Steigung) nicht in IR \ {0}, also nicht in ganz ID
fällt (negative Steigung) nicht in IR \ {0}, also nicht in ganz ID
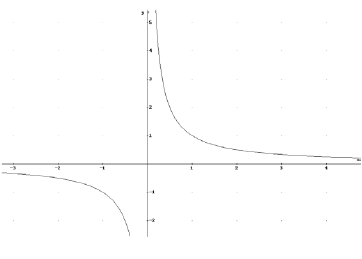
- beachtet man zunächst gesondert den Bereich IR-,
so ist die Funktion streng monoton abnehmend, da gilt: x2
↔ f(x1) <
f(x2)
- die streng monotone Abnahme der Funktion gilt
auch im Bereich R+, da auch hier gilt:
x2 ↔ f(x1)
< f(x2)
- betrachtet man die Funktion aber in IR \ {0} so
ist sie nicht streng monoton abnehmend, da x1 > x2
und f(x1) > f(x2) möglich ist.
0,5 > -2 und 2> -0,5
Tatsache 6
Anzahl der Nullstellen eines Polynoms
Ein Polynom vom Grad n hat höchstens n Nullstellen.
Beweisidee:
f(x) = x4 - 2x³ +
3x²+ 2x -4 ist ein Polynom
4. Grades
Kennt man eine Nullstelle z.B. x = 1 so kann man mittels Polynomdivision den
Funktionsterm durch (x - 1) teilen:
f(x) = x4 - 2x³ + 3x²+ 2x -4 : (x - 1) = x³
- x² + 2x + 4
Das Ergebnis hat jetzt nur noch den Grad 3
Danach würde man für das Ergebnis der Polynomdivision weiter nach
Nullstellen suchen und z.B. x = -1 finden.
Bei der nächsten Polynomdivision erniedrigt sich das Ergebnis wieder um
einen Grad.
x³ - x² + 2x + 4 : (x + 1) = x² -2x + 4
Dieses Ergebnis hat jetzt noch höchstens 2 Nullstellen.
Da sich also für jede gefundene
Nullstelle der Grad des Ergebnisses um eins erniedrigt, hat das Polynom
höchstens so viele Nullstellen wie der Grad angibt.
Tatsache 7
Verhalten des Graphen beim Durchgang durch die
Nullstelle
Beispiel:
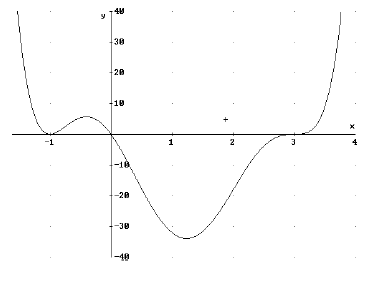
f(x) = x * (x + 1)² * ( x - 3)³
einfache Nullstelle bei x =0
Vorzeichenwechsel des Graphen
doppelte Nullstelle bei x = -1
Graph berührt die x- Achse
dreifache Nullstelle bei x = 3
Graph schneidet wieder die x- Achse
Allgemein:
- wenn n gerade, Nullstelle ohne Vorzeichenwechsel, d.h. der
Graph berührt nur die x- Achse
- wenn n ungerade, Nullstelle mit Vorzeichenwechsel, d.h. der
Graph schneidet die x- Achse
Wann wechselt eine stetige Funktion das Vorzeichen?
- bei Nullstellen gerader Ordnung
- bei Polstellen ungerader Ordnung
Bei Nullstellen gerader Ordnung berührt der Graph die x- Achse nur.
Tatsache 8
Symmetrien bei den Graphen von Polynomfunktionen
Der Funktionsterm enthält nur gerade Potenzen von x
→
der Graph ist achsensymmetrisch zur y-Achse, für
gerades n gilt also: xn = (-xn)
Bei diesen Funktionen ist
f(-x) = f(x) 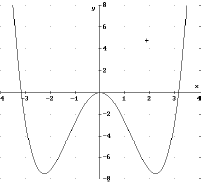
Beispiel:
f(x) = 0,3x4 -
3x²
f(-x) = 0,3(-x)4 - 3(-x)² = 0,3x4
- 3x² = f(x)
Wenn f(x) = f(-x) muss der Graph achsensymmetrisch
sein.
Der Funktionsterm enthält nur ungerade Potenzen von x
→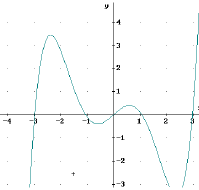
Der Graph ist punktsymmetrisch.
Betrachtet man eine Funktion mit nur ungeraden
Potenzen, so ist f(-x) = - f(x)
d.h. ihr Graph ist punktsymmetrisch zum Ursprung.
Der Symmetriepunkt ist der Ursprung
Beispiel:
f(x) = 0,1x5 - x³ + x
Tatsache 9
Veränderungen von Graphen f(-x),
-f(x), f(x)+a, f(x+a)
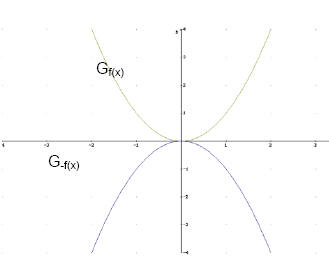
-f(x)
Beispiel:
f(x) = x²
-f(x) = -x²
Wird der ganze Funktionsterm mit -1 multipliziert,
dann wird der Graph an der x- Achse gespiegelt
f(-x)
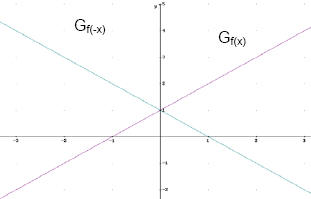
Beispiel:
f(x) = x + 1
f(-x) = -x + 1
Wird nur das x mit -1 multipliziert, dann wird der
Graph an der y- Achse gespiegelt
Deswegen auch Tatsache 8:
Wenn für den Funktionsterm gilt: f(-x) = f(x) dann ist der Graph
achsensymmetrisch zur y- Achse
f(x) + a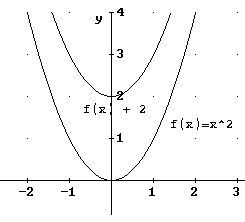
Besipiel:
f(x) = x²
f(x) + a = x² + 2
Wird eine Konstante k zum Funktionsterm addiert, so
wird der Graph um diese Konstante nach oben (k>0) oder nach unten (k<0)
verschoben.
f(x+a)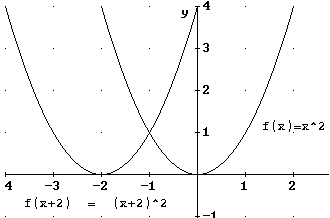
Besipiel:
f(x) = x²
f(x+a) = (x+2)²
Wird die Konstante k nur zum x addiert, so wird der
Graph nach rechts (k<0) oder nach links (k>0) verschoben.
Die Richtung der Verschiebung ist also gerade umgekehrt als das Vorzeichen
von a. Man kann sich das gut an den Nullstellen der beiden Funktionen f(x) =
(x+2)² und f(x) = (x-2)² merken.
Tatsache 10
Gebrochen rationale Funktionen
10.1
Definitionsbereich = IR \ {Nullstellen des Nenners}
10.2 Löcher des Graphen sind
Gleichzeitig Nullstellen von Zähler und Nenner
(hebbare Definitionslücken)
10.3 Nullstellen der Funktion = Nullstellen
des Zählers der gekürzten Fassung,
senkrechte Asymtoten haben die Gleichung x = (solch eine Z-Nullstelle)
10.4 Polstellen der Funktion = Nullstellen
des Nenners der gekürzten Fassung
10.5 Waagrechte Asymptoten: Wenn Grad Z =
Grad N, sonst schiefe asymptotische
Geraden oder auch Kurven (letzteres, wenn Grad Z um 2 größer als Grad N)
Tatsache 11
Steigung von f in xo
Um die Steigung in einem Punkt P eines
Funktionsgraphen zu ermitteln, bildet man zuerst die Sekante durch diesen
Punkt P und einen Punkt Q.
Formel:
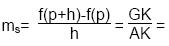
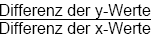
Beispiel:
f(x) = x² im Punkt (1/1)
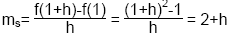
Die Sekantensteigung beschreibt die durchschnittliche
Steigung eines Abschnitts der Funktion zwischen zwei Punkten.
Nun geht man zur Tangente über, indem der Abstand der
zwei Schnittpunkte der Sekante mit dem Graphen immer kleiner wird:
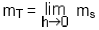
→ Steigung in einem Punkt der
Funktion
Der Grenzwert der Sekante ist n
- die Tangentensteigung ist n
- die Funktion hat für p die Steigung n
- f' (p) = n
Inzwischen kennen wir natürlich die Steigungsformel
f'(x) für jeden x- Wert der Parabel: f'(x) = 2x Also müssen wir nur noch
einen x- Wert in die Steigungsformel einsetzten um die Steigung zu
ermitteln, z.B. f'(1) = 2 * 1 = 2
Das ist dann natürlich auch gleichzeitig der
Steigungswert m der Tangente an die Parabel im Punkt (1/1)
Allgemeine Definition:

Tatsache 12
Wichtige Ableitungsregeln: sin/ cos, Produkt und
Kettenregel
12.1 Ableitung
von sinus- und cosinus-
Funktionen
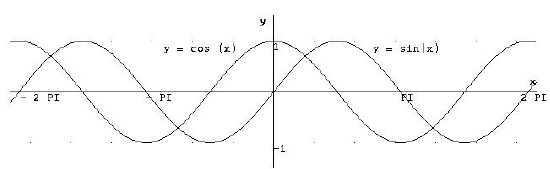
Grund warum der sin (x) abgeleitet der cos (x) ist:
Betrachtet man den cos (x) stellt man fest, dass er
bei 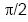 einen
Vorzeichenwechsel (VzW) einen
Vorzeichenwechsel (VzW)
+ → - hat, was auf ein Maximum der Sinusfunktion schließen lässt.
Auch an der Stelle 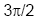 , wo
ein VzW - → + der
Cosinusfunktion stattfindet, besitzd die Funktion sin(x) einen Tiefpunkt. , wo
ein VzW - → + der
Cosinusfunktion stattfindet, besitzd die Funktion sin(x) einen Tiefpunkt.
Außerdem muss die Ableitung der Funktion sin(x) periodisch sein.
All diese Kriterien erfüllt der cos(x).
Analog dazu kann diese Betrachtung auch bei cos(x), -sin(x)
und -cos(x) durchgeführt werden.

12.2 Produktregel
f(x) = u(x)`* v(x)
f'(x) = u(x) * v'(x) + v(x) * u'(x)
Was
u oder v ist ist bei der Produktregel egal!
Beispiel:
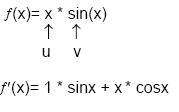
12.3 Quotientenregel
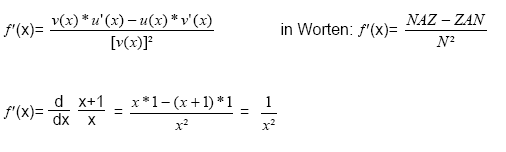
12.4 Kettenregel
f(x) = v'(u(x)) * u'(x)
in Worten: äußere Ableitung mal innere Ableitung
Das vergessene Nachdifferenzieren
ist einer der beliebtesten Fehler!
Beispiel:
f(x) = (3x - 2)²
u(x) = 3x -2 = z
v(z) = z²
v(u(x)) = (3x - 2)²
f'(x) = 2 * z² * 3 = 2 * (3x -2) * 3 = 18x - 12
Tatsache 13
Monotoniekriterium: Bestimmung der Steigung mit
Hilfe von f
Geg: f(x) = x4
Ges: Monotonie, Steigung (f)
Lösung:
a)

b)

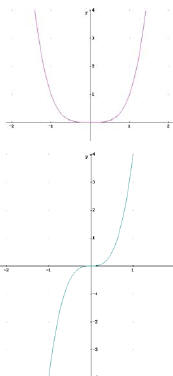
Beispiel:
f(x) = x4
Tatsache 14
Extrempunkte und Sattelpunkte
14.1 Waagrechte Tangenten
Wenn die erste Ableitung Null an einer Stelle ist, dann hat der Graph
eine Waagrechte Tangente.
Ob weiterhin ein Extrempunkt oder ein Sattelpunkt vorliegt, muss erst
untersucht werden.
Beispiel: f(x) = 0, aber kein Extrempunkt
Gegeben ist die Funktion:
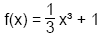
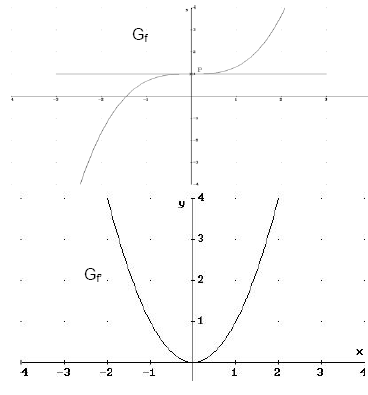
Wir bilden die erste Ableitung:
f'(x) = x². f' hat eine Nullstelle bei x = 0,
aber es liegt bei x= 0 kein Extrempunkt vor,
da die Funktion f' ihr Steigungsverhalten
nicht wechselt.
Es liegt ein sogenannter Sattelpunkt vor.
Da die Ableitung an einer Stelle Null ist, hat der
Graph dort eine waagrechte Tangente, wie die Skizze verdeutlicht.
Berechnung der Tangente in P(0/1)
mt = f'(0) = 0
Tangente: y = 0 * x + t
t ist hier der y- Wert von P,
also y = 1
Sattelpunkt (SAP)/ Terrassenpunkt (TEP)
f ' hat eine Nullstelle ohne Vorzeichenwechsel
f '' hat eine Nullstelle mit Vorzeichenwechsel
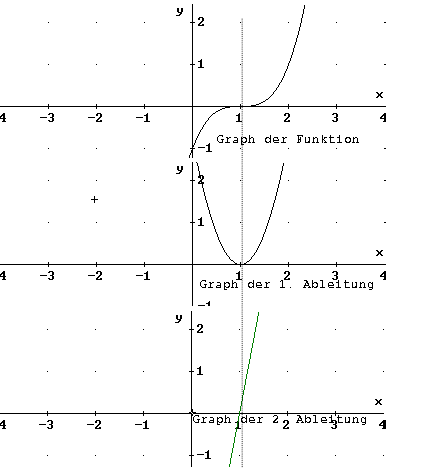
Hieraus folgt, dass Sattelpunkte auch automatisch
Wendepunkte sind.
Minimum/ Maximum
f ' hat eine Nullstelle mit Vorzeichenwechsel
f '' hat keine Nullstelle
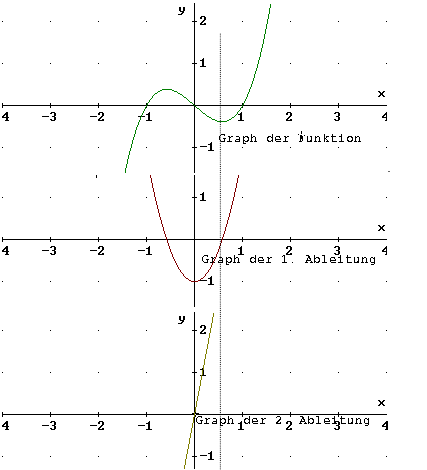
Maximum (Max)
y- Wert des Hochpunktes
Minimum (min)
y- Wert des Tiefpunktes
Beispiel:
f(x) = x³ -3x² = x² (x - 3) Nullstellen: (0/0),
(3/0)
f'(x) = 0
f'(x) = 3x² - 6x
3x² - 6x = 0
f'(x) = x (3x - 6) = 0
Punkt1: x1 = 0
Punkt2: x2 = 2
y2 = 0
y2 = -4
Graph von f hat bei x = 0 und y = 2 waagrechte
Tangenten, aber noch kein Minimum gezeigt.
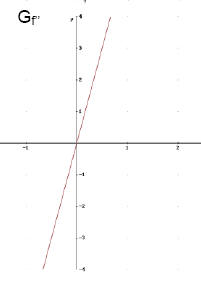
Nachweis für Minimum: Skizze von Gf'
f' hat bei x = 2 VzW + → -
f hat bei x = 2 ein relatives Minimum.

14.2 Extrempunkte ohne Ableitung
Es gibt auch Extrempunkte, ohne dass die erste
Ableitung Null ist:
nämlich wenn Gf einen Knick hat und f' nicht existiert.
Beispiel:
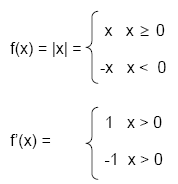
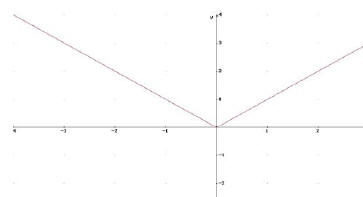
für x = 0 existiert keine Ableitung
Wie könnte eine Argumentation für TIP aussehen?
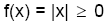 Der kleinstmögliche
Funktionswert ist als Null. Der kleinstmögliche
Funktionswert ist als Null.
Bei x = 0 gilt f(x) = 0 die Funktion nimmt sogar ein absolutes
Minimum an.
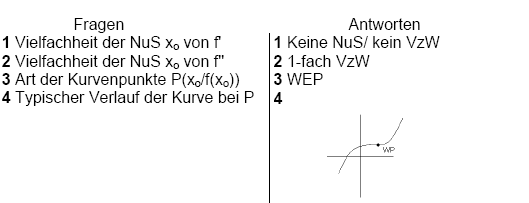
Tatsache 15
Wendepunkte
Der Übergang von Rechts- auf Linkskrümmung
(beziehungsweise umgekehrt), heißt Wendepunkt (WEP). Wendepunkte liegen an
den Extrempunkten von f' bzw. an den Nullstellen mit VzW von f''.
Tatsache 16
Krümmung
f' positiv →
Graph linksgekrümmt
f' negativ → Graph rechtsgekrümmt
Beispiel:
Gegeben ist die Funktion: f(x) = x³ -3x = x (x² - 3)
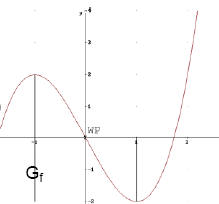
1. Ableitung: f' (x) = 3 ( x² -1) = 3x² - 3
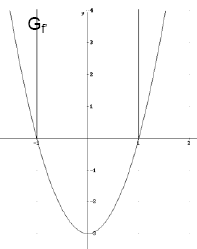
2. Ableitung: f''(x) = 6x
x < 0: f''(x) < 0
→ Gf rechtsgekrümmt
x = 0: f''(x) hat VzW → Gf hat
Wendepunkt
x > 0: f''(x) > 0
→ Gf linksgekrümmt
Tatsache 17
Welche Funktion steigt stetig?
Stetig sind im Bereich der Schulmathematik alle
Funktionen, die sich durch eine einzige Funktionsgleichung darstellen
lassen, auch Funktionen mit Beträgen.
(Stetigkeit bedeutet: Die Funktion kann durchgezeichnet werden, besitzt also
keine Lücken.)
Die Stetigkeit von abschnittsweise definierten
Funktionen an ihren Nahtstellen muss nachgeprüft werden.
Tatsache 18
Differenzierbarkeit und Stetigkeit
Ist eine Funktion differenzierbar an einer Stelle xo,
dann ist sie dort auch stetig (gewesen).
Wenn eine Funktion also stetig an einer Stelle xo ist, dann kann
sie differenzierbar sein oder nicht.
Beispiel: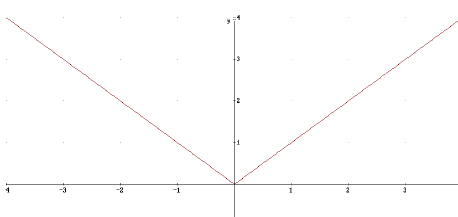
f(x) = IxI
stetig in x = 0
(Graph hat keinen Sprung)
aber nicht differenzierbar
in x = 0
( Graph hat einen Knick)
Tatsache 19
Sprünge und Knicke bei Graphen
18.1 Sprünge
Ist f nicht stetig an einer Stelle im
Definitionsbereich, so hat der Graph dort einen Sprung
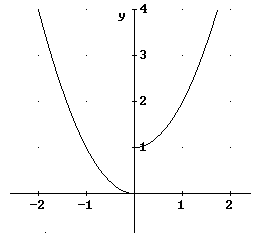
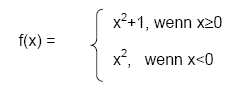
Dies gilt nicht für Definitionslücken, z.B.
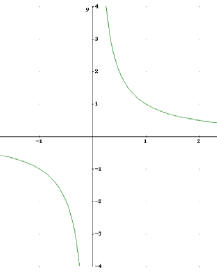

Gf springt bei x = 0
f nicht unstetig bei x = 0,
denn x = 0 existiert für f nicht!
f ist aber natürlich auch nicht stetig bei x = 0!
18.2 Knicke
ist f nicht differenzierbar an einer stelle aus IDf,
an der f stetig ist, so hat der Graph dort einen Knick
Beispiel: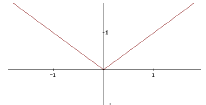
f (x) 0 IxI
Dies ist nicht anwendbar auf Stellen, an denen f noch
nicht mal stetig ist. Denn hat der Graph einen Sprung, dann kann man gar
nicht nach einem Knick fragen.
|
